Итак, давайте возьмем да и представим, что мы получили «железо» некоего универсального гражданского робота. Это может быть андроид, с фантастической точностью повторяющий движения человеческого тела. Или же некий модуль, имеющий возможность объединяться с другими модулями для исполнения полезной работы. Даже крупный андроид в силу универсальности может производиться массово – миллиардами штук – что сделает его дешевым и доступным. А уж модули станут производиться партиями, для которых трудно вспомнить числительные…
Ничего невозможного тут нет, законам природы сие не противоречит. И тогда – во вполне обозримом будущем – встанет задача научить это «железо» совершать некие полезные действия. Ведь только тогда оно превратится в товар, который можно будет продать, да к тому же продать в массовых количествах. И как же будет протекать эта учеба?
Ну, раньше – в индустриальную эпоху – дело обстояло так. Динамике и кинематике машины «учили» инженеры, «учили» процедурным навыкам исходя из декларативных знаний. Нет-нет, бывали, конечно, и изобретатели-самоучки. Те самые, которых воспел в «Городе Градов» Андрей Платонов:
Комиссия решила, что технического персонала на рынке республики нет, и по одному доброму совету приняла, что эти работы надо поручить бывшим солдатам-военнопленным, а также сельским самоучкам, которые даже часы могут чинить, а не только насыпь сделать или яму для воды выкопать. Один член этой приемочной комиссии вслух прочитал книгу, где говорится, как холоп Микишка сделал аэроплан и летал на нем перед Иваном Грозным, чем убедил окончательно комиссию в скрытых силах пролетариата и трудового крестьянства. Следовательно, решила комиссия, средства, отпущенные губернии на борьбу с недородом, помогут “выявить, использовать, учесть и в дальнейшем снова использовать внутренние умственные силы пролетариата и беднейших крестьян, тем самым гидротехнические работы в нашей губернии будут иметь косвенный культурный эффект”.
Было построено шестьсот плотин и четыреста колодцев. Техников совсем не было, а может, было человека два. Не достояв до осени, плотины были смыты летними легкими дождями, а колодцы почти все стояли сухими.
Так вот, чтобы избежать подобных конфузов, создание машин поручалось инженерам. Тем, которые в средней школе учили законы Ньютона. Кстати, одно из глубочайших массовых (ну – в смысле тех немногих людей, кого это интересует) заблуждений состоит в том, что математика «по Киселеву» исключала изучение математического анализа в курсе средней школы, а привнесен он туда был уже «по Колмогорову». А это – не так. Еще в 1911 году у Киселева вышло «Начальное учение о производных для 7-го класса реальных училищ». Ведь крайне важно дать детям, к тому моменту, когда они приступят к законам Ньютона понятие о производных, делающих эти законы предельно ясными.
Но это – школа. Потом был вуз. В традиционном курсе инженерного образование последовательно шли общая физика и теоретическая механика. К законам Ньютона добавлялись формула Эйлера, принцип д’Аламбера, уравнение Мещерского и теорема вириала. Учебники были разные, от объемистых Бухгольца и Ландау-Лифшица до лаконичного Тарга, но задачник один, уникальное – хоть и ведомое лишь инженерам – явление отечественной культуры, увидевший свет в 1911 году «Сборник задач по теоретической механике» И. В. Мещерского.
А вот потом уже переходили к железкам. Которые надо было рассмотреть и изучить, ну а потом описать системой дифференциальных уравнений. Причем надо было стараться, чтобы уравнения эти были обыкновенными, а до появления достаточно мощных ЭВМ вообще линейными. После того, как система уравнений составлялась, она обсчитывалась. В совсем древние, довоенные времена – на бумаге, в квадратурах. Потом – на аналоговых машинах, каких-нибудь МН-7, с выводом результатов на шлейфовый осциллограф (стрелки в нем не было, рисовал он ультрафиолетовым зайчиком на фотобумаге).
Ну а уж потом – на цифровых ЭВМ, «Минсках» или ЕС-1022, с распечаткой результатов на оберточной бумаге (финская специализированная была в дефиците)… И в любом случае результаты расчетов сравнивались с результатами, снятыми с железки – будь то планер управляемого снаряда или качающаяся часть артиллерийской системы – при физическом моделировании. Если они различались – подгонялись коэффициенты (которые без зазрения совести варьировались в пределах 0,1-100…), уточнялась структура уравнений…
А потом уже, глядя на эту структуру уравнений, начинало синтезироваться управление. Или простейшее, по отклонениям или пропорциональное, которое искали методами линейной теории автоматического уравнения, на основе полупартизанских операторов Хевисайда и несколько более лучше определенных Лапласа. Или оптимальное, по Понтрягину скажем, когда речь шла о том, чтобы доставить к удаленной точке какой-то массивный полезный груз (по воспоминаниям А.П.Казанцева в первом варианте «Туманности Андромеды» была глава «Веда раскапывает Нью-Йорк»).
Но всегда и везде – начиная с первых автопилотов Сперри, систем управления крылатых ракет FZG 76 и ракет баллистических Aggregat-4 – прежде чем наделить машину, динамический объект, процедурными навыками, «научить» ее что либо делать, инженеры вырабатывали декларативные знания об этом объекте, в пространстве математики строили его описания на языке уравнений и коэффициентов.
И вот теперь появилась возможность избежать этапа декларативного описания динамических объектов в процессе синтеза управления ими. Котенок же, обучаясь оперировать лапками и выпускать коготки, не имеет ни малейшего представления ни о ньютоновой механике, не о биохимических и биофизических процессах, ответственных за сокращение его мускулов, и передачу сигналов по нервам. Да и кошка, обучая отпрыска ловле мышей или голубей, ну совсем ничего не знает о дифференциальной теории игр.
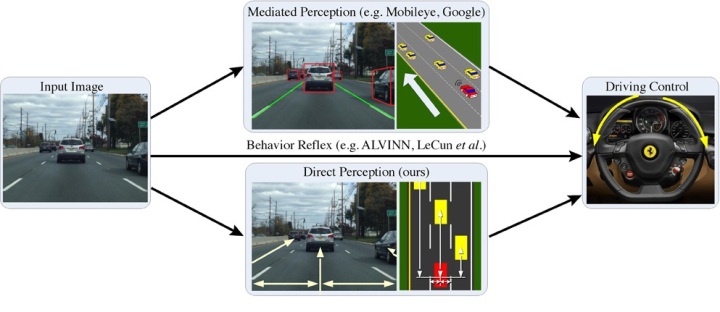
И вот теперь такая возможность – дарованная Большими Данными и Глубоким Обучением – появляется и в мире машин. Об этом рассказывает статья DeepDriving: Learning Affordance for Direct Perception in Autonomous Driving. Термин DeepDriving , ГлубокоеВождение, образовано тут по аналогии с Deep Learning. Точно так же, как нейросеть не программируется, а обучается, сама формируя свои коэффициенты и связи, так и тут, свернутая нейросеть, Convolutional Neural Network, на которую подается видеопоток, самостоятельно обучается вождению.
Нет, нет, пугаться не надо – на улицы городов динамическую модель с простеньким (по меркам нейронаук!) контроллером не выпускали. Она тренировалась в видеоиграх, за дюжину часов «вождения» достигнув вполне приемлемого уровня. Но, как делается вывод в статье, такой подход может быть применен и к реальным динамическим объектам, оперирующим в реальной среде, представленной изображениями. В потоке дорожного движения, в заводском цеху или складе дистрибьюторской компании, при уборке квартиры и расстановке товара по магазинным полкам.
То есть, речь может идти (да-да, может и не идти, на ранних этапах развития технологий трудно судить, что именно окажется в роли killer application, вон, первое издание Малой Советской Энциклопедии рассказывало об автожирах, о роторных парусниках, но и о жидких кристаллах – это в 1930-м году!!!) о фантастическом повышении производительности инженерного труда в части создания систем управления сложными динамическими объектами, такими как универсальный робот.
А это может преобразовать весь мир работы с материальными объектами ничуть не слабее, чем цифровая революция, резкое повышение производительности изготовления цифровых схем и тиражирования программного обеспечения управления ими преобразовало весь мир работы с информацией. С труднопредсказуемыми последствиями для всего планетарного социума…